Generic Extended Kalman Filter (EKF) template base class. More...
#include <ekfilter.hpp>

Public Types | |
| enum | { beg = BEG } |
| typedef KMatrix< T, BEG, DBG > | Matrix |
| Matrix type. | |
| typedef T | type |
| Type of objects contained in matrices and vectors. | |
| typedef KVector< T, BEG, DBG > | Vector |
| Vector type. | |
Public Member Functions | |
| void | init (Vector &x_, Matrix &P_) |
| Sets initial conditions for the Kalman Filter. | |
Kalman Filter Functions | |
These functions allow to get the results from the Kalman filtering algorithm. Before any of these can be called, all dimensions must have been set properly at least once and | |
| const Matrix & | calculateP () const |
| Returns the a posteriori error covariance estimate matrix. | |
| const Vector & | getX () const |
| Returns the corrected state (a posteriori state estimate). | |
| void | measureUpdateStep (const Vector &z_) |
| Makes one correction step. | |
| const Vector & | predict (Vector &u_) |
| Returns the predicted state vector (a priori state estimate). | |
| const Vector & | simulate () |
| Returns the predicted measurement vector. | |
| void | step (Vector &u_, const Vector &z_) |
| Makes one prediction-correction step. | |
| void | timeUpdateStep (Vector &u_) |
| Makes one prediction step. | |
Constructor and Destructor. | |
| EKFilter (K_UINT_32 n_, K_UINT_32 nu_, K_UINT_32 nw_, K_UINT_32 m_, K_UINT_32 nv_) | |
| Constructors specifying all necessary matrix and vector dimensions. | |
| EKFilter () | |
| Default constructor. | |
| virtual | ~EKFilter () |
| Virtual destructor. | |
Dimension Accessor Functions | |
| K_UINT_32 | getSizeU () const |
| Returns the size of the input vector. | |
| K_UINT_32 | getSizeV () const |
| Returns the size of the measurement noise vector. | |
| K_UINT_32 | getSizeW () const |
| Returns the size of the process noise vector. | |
| K_UINT_32 | getSizeX () const |
| Returns the size of the state vector. | |
| K_UINT_32 | getSizeZ () const |
| Returns the size of the measurement vector. | |
Resizing Functions | |
These functions allow to change the dimensions of all matrices and vectors, thus implementing a Variable-Dimension Extended Kalman Filter. They do nothing if the new size is the same as the old one.
| |
| void | setDim (K_UINT_32 n_, K_UINT_32 nu_, K_UINT_32 nw_, K_UINT_32 m_, K_UINT_32 nv_) |
| Sets all dimensions at once. | |
| void | setSizeU (K_UINT_32 nu_) |
| Sets the size of the input vector. | |
| void | setSizeV (K_UINT_32 nv_) |
| Sets the size of the measurement noise vector. | |
| void | setSizeW (K_UINT_32 nw_) |
| Sets the size of the process noise vector. | |
| void | setSizeX (K_UINT_32 n_) |
| Sets the size of the state vector. | |
| void | setSizeZ (K_UINT_32 m_) |
| Sets the size of the measurement vector. | |
Protected Member Functions | |
| void | NoModification () |
| Allows optimizations on some calculations. | |
| virtual void | sizeUpdate () |
| Resizes all vector and matrices. Never call or overload this ! | |
Matrix Creators | |
Theses functions have been designed to be overridden by derived classes if necessary. Their role is to fill in the parts of the Kalman matrices that change between iterations. That is to say, these functions should set values inside matrices that depend on x or u. These functions can suppose that their corresponding matrix pre-creator has been called at least once before. Also,
| |
| virtual void | makeA () |
| Virtual creator of A. | |
| virtual void | makeCommonMeasure () |
| Optional function used to precalculate common values for measurement. | |
| virtual void | makeCommonProcess () |
| Optional function used to precalculate common values for process. | |
| virtual void | makeDZ () |
| Hook-up function to modify innovation vector. | |
| virtual void | makeH () |
| Virtual creator of H. | |
| virtual void | makeMeasure ()=0 |
Actual measurement function 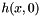 . Fills in z. . Fills in z. | |
| virtual void | makeProcess ()=0 |
Actual process 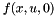 . Fills in new x by using old x. . Fills in new x by using old x. | |
| virtual void | makeQ () |
| Virtual creator of Q. | |
| virtual void | makeR () |
| Virtual creator of R. | |
| virtual void | makeV () |
| Virtual creator of V. | |
| virtual void | makeW () |
| Virtual creator of W. | |
Matrix Pre-Creators | |
Theses functions have been designed to be overridden by derived classes if necessary. Their role is to fill in the parts of the Kalman matrices that don't change between iterations. That is to say, these functions should only set constant values inside matrices that don't depend on x or u. They will all be called at least once, before the calls to their corresponding matrix (not pre-) creators. In fact, they are called once per resize (not necessarily at the moment of the resize though), including while the matrices are first allocated.
| |
| virtual void | makeBaseA () |
| Virtual pre-creator of A. | |
| virtual void | makeBaseH () |
| Virtual pre-creator of H. | |
| virtual void | makeBaseQ () |
| Virtual pre-creator of Q. | |
| virtual void | makeBaseR () |
| Virtual pre-creator of R. | |
| virtual void | makeBaseV () |
| Virtual pre-creator of V. | |
| virtual void | makeBaseW () |
| Virtual pre-creator of W. | |
Protected Attributes | |
Kalman Vectors and Matrices | |
| Matrix | A |
| A jacobian matrix. | |
| Vector | dz |
| Innovation vector. | |
| Matrix | H |
| A jacobian matrix. | |
| Matrix | Q |
| Process noise covariance matrix. | |
| Matrix | R |
| Measurement noise covariance matrix. | |
| Vector | u |
| Input vector. | |
| Matrix | V |
| A jacobian matrix. | |
| Matrix | W |
| A jacobian matrix. | |
| Vector | x |
| Corrected state vector. | |
| Vector | z |
| Predicted measurement vector. | |
Kalman Dimensions | |
| K_UINT_32 | m |
| Size of the measurement vector. | |
| K_UINT_32 | n |
| Size of the state vector. | |
| K_UINT_32 | nu |
| Size of the input vector. | |
| K_UINT_32 | nv |
| Size of the measurement noise vector. | |
| K_UINT_32 | nw |
| Size of the process noise vector. | |
Private Member Functions | |
| void | measureUpdate (T dz, T r) |
| U-D convariance factorization update. | |
| void | timeUpdate () |
| MWG-S orthogonalization algorithm for U-D time update. | |
Template Methods | |
These are all template methods (in a design pattern sense, these are not template member functions). They simply call their corresponding virtual not-Impl functions, but adding some logic to take into account the | |
| void | makeAImpl () |
makeA() template method. | |
| void | makeBaseAImpl () |
makeBaseA() template method. | |
| void | makeBaseHImpl () |
makeBaseH() template method. | |
| void | makeBaseQImpl () |
makeBaseQ() template method. | |
| void | makeBaseRImpl () |
makeBaseR() template method. | |
| void | makeBaseVImpl () |
makeBaseV() template method. | |
| void | makeBaseWImpl () |
makeBaseW() template method. | |
| void | makeHImpl () |
makeH() template method. | |
| void | makeQImpl () |
makeQ() template method. | |
| void | makeRImpl () |
makeR() template method. | |
| void | makeVImpl () |
makeV() template method. | |
| void | makeWImpl () |
makeW() template method. | |
Static Private Member Functions | |
| static void | factor (Matrix &P_) |
| Inplace upper triangular matrix Cholesky (UDU) factorization. | |
| static void | upperInvert (Matrix &P_) |
| Inplace upper triangular matrix inversion. | |
Private Attributes | |
| Matrix | _P |
| Temporary matrix. | |
| Vector | _x |
| Vector | a |
| Temporary vector. | |
| Vector | d |
| Temporary vector. | |
| K_UINT_16 | flags |
| Temporary vector. | |
| Matrix | H_ |
| Modified version of H to whiten measure noise. | |
| bool | modified_ |
Boolean flag used by NoModification(). | |
| K_UINT_32 | nn |
| Number of columns of U. | |
| Matrix | Q_ |
| Modified version of Q to whiten process noise. | |
| Matrix | R_ |
| Modified version of R to whiten measure noise. | |
| Matrix | U |
| Cholesky factorization of P. | |
| Vector | v |
| Temporary vector. | |
| Matrix | W_ |
| Modified version of W to whiten process noise. | |
Generic Extended Kalman Filter (EKF) template base class.
EKFilter-derived class freely : this can be useful if you need to branch your filter based on some condition.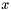 (to estimate) and a non-linear process function
(to estimate) and a non-linear process function 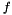 (to model) that describes the evolution of this state through time, that is :
(to model) that describes the evolution of this state through time, that is :
![\[ x_k = f \left( x_{k-1}, u_{k-1}, w_{k-1} \right) \]](form_38.png)
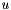 is the (known) input vector fed to the process and
is the (known) input vector fed to the process and 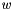 is the (unknown) process noise vector due to uncertainty and process modeling errors. Further suppose that the (known) process noise covariance matrix is :
is the (unknown) process noise vector due to uncertainty and process modeling errors. Further suppose that the (known) process noise covariance matrix is :
![\[ Q = E \left( w w^T \right) \]](form_39.png)
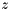 , which depends on the current state
, which depends on the current state 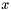 in the form of a non-linear function
in the form of a non-linear function 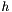 (to model) :
(to model) :
![\[ z_k = h \left( x_k, v_k \right) \]](form_41.png)
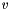 is the (unknown) measurement noise vector with a (known) covariance matrix :
is the (unknown) measurement noise vector with a (known) covariance matrix :
![\[ R = E \left( v v^T \right) \]](form_42.png)
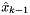 , called a corrected state or an a posteriori state estimate. We can build a predicted state (also called an a priori state estimate) by using
, called a corrected state or an a posteriori state estimate. We can build a predicted state (also called an a priori state estimate) by using 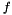 :
:
![\[ \tilde{x}_k = f \left( \hat{x}_{k-1}, u_{k-1}, 0 \right) \]](form_44.png)
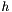 :
:
![\[ \tilde{z}_k = h \left( \tilde{x}_k, 0 \right) \]](form_45.png)
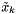 :
:
![\[ x_k \approx f \left( \hat{x}_{k-1}, u_{k-1}, 0 \right) //! + \frac{\partial f}{\partial x} \left( \hat{x}_{k-1}, u_{k-1}, 0 \right) //! \left( \Delta x \right) //! + \frac{\partial f}{\partial u} \left( \hat{x}_{k-1}, u_{k-1}, 0 \right) //! \left( \Delta u \right) //! + \frac{\partial f}{\partial w} \left( \hat{x}_{k-1}, u_{k-1}, 0 \right) //! \left( \Delta w \right) \]](form_47.png)
![\[ \phantom{x_k} = \tilde{x}_k + A \left( x_{k-1} - \hat{x}_{k-1} //! \right) + W w_{k-1} \]](form_48.png)
![\[ z_k \approx h \left( \tilde{x}_k, 0 \right) //! + \frac{\partial h}{\partial x} \left( \tilde{x}_k, 0 \right) //! \left( \Delta x \right) //! + \frac{\partial h}{\partial v} \left( \tilde{x}_k, 0 \right) //! \left( \Delta v \right) \]](form_49.png)
![\[ \phantom{z_k} = \tilde{z}_k + H \left( x_k - \tilde{x}_k \right) //! + V v_k \]](form_50.png)
T : Type of elements contained in matrices and vectors. Usually float or double.BEG : Starting index of matrices and vectors. Can be either 0 or 1.OQ : Optimize calculations on Q. This can be turned on if Q is diagonal.OVR : Optimize calculations on V and R. This can be turned on if V and R are both diagonal matrices.DGB : Debug flag. If true, then bound-checking will be performed, and OutOfBoundError exceptions can be thrown.T must be default constructible.T must be constructible from double.T must be assignable.T must be equality comparable.T must be serializable.T must support basic arithmetic operations.t1, t2 are instances of T, op is an arithmetic operator (+ - * /), is is of type istream and os is of type ostream, the following expressions must be valid :T(); T t1;
T(0.0); T t1(1.0);
double T t1 = t2; T t1(t2); T(t1);
t1 op t2
T -t1
T. Same as : T(0.0) - t1;
t1 = t2;
t1 op= t2;
t1 = t1 op t2;
t1 == t2
bool is >> t1;
operator>>() os << t1;
operator<<() Finally, note that operator>>() and operator<<() must be compatible. Also, operator&() must not have been overloaded.
Definition at line 150 of file ekfilter.hpp.
| typedef KMatrix<T, BEG, DBG> Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::Matrix |
Matrix type.
Definition at line 44 of file ekfilter.hpp.
| typedef T Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::type |
Type of objects contained in matrices and vectors.
Definition at line 38 of file ekfilter.hpp.
| typedef KVector<T, BEG, DBG> Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::Vector |
Vector type.
Definition at line 43 of file ekfilter.hpp.
| anonymous enum |
Definition at line 40 of file ekfilter.hpp.
| Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::EKFilter | ( | ) | [inline] |
Default constructor.
Definition at line 96 of file ekfilter_impl.hpp.
| Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::EKFilter | ( | K_UINT_32 | n_, | |
| K_UINT_32 | nu_, | |||
| K_UINT_32 | nw_, | |||
| K_UINT_32 | m_, | |||
| K_UINT_32 | nv_ | |||
| ) | [inline] |
Constructors specifying all necessary matrix and vector dimensions.
This constructor simply calls setDim() with all the corresponding arguments.
Definition at line 102 of file ekfilter_impl.hpp.
| Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::~EKFilter | ( | ) | [inline, virtual] |
Virtual destructor.
Definition at line 110 of file ekfilter_impl.hpp.
| const KTYPENAME EKFilter< T, BEG, OQ, OVR, DBG >::Matrix & Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::calculateP | ( | ) | const [inline] |
Returns the a posteriori error covariance estimate matrix.
Definition at line 431 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::factor | ( | Matrix & | P_ | ) | [inline, static, private] |
Inplace upper triangular matrix Cholesky (UDU) factorization.
This function is based on an algorithm in presented in appendix III.A in [01]. It is used to transform P_ into 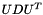 . Quoting from [01] : "This mechanization is such that the lower portion of
. Quoting from [01] : "This mechanization is such that the lower portion of P_ is not used and U and D can share the upper triangular portion of P_ (the diagonal elements of U are implicitly unity). In any case the upper triangular portion of P is destroyed by this mechanization."
Definition at line 628 of file ekfilter_impl.hpp.
| K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::getSizeU | ( | ) | const [inline] |
Returns the size of the input vector.
Definition at line 129 of file ekfilter_impl.hpp.
| K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::getSizeV | ( | ) | const [inline] |
Returns the size of the measurement noise vector.
Definition at line 144 of file ekfilter_impl.hpp.
| K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::getSizeW | ( | ) | const [inline] |
Returns the size of the process noise vector.
Definition at line 134 of file ekfilter_impl.hpp.
| K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::getSizeX | ( | ) | const [inline] |
Returns the size of the state vector.
Definition at line 124 of file ekfilter_impl.hpp.
| K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::getSizeZ | ( | ) | const [inline] |
Returns the size of the measurement vector.
Definition at line 139 of file ekfilter_impl.hpp.
| const KTYPENAME EKFilter< T, BEG, OQ, OVR, DBG >::Vector & Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::getX | ( | ) | const [inline] |
Returns the corrected state (a posteriori state estimate).
Definition at line 426 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::init | ( | Vector & | x_, | |
| Matrix & | P_ | |||
| ) | [inline] |
Sets initial conditions for the Kalman Filter.
This function allows to set an initial state estimate vector and an initial error covariance matrix estimate. This must be called at least once, after all dimensioning functions and before any other function. However, it can also be called anytime to reset or modify x or P.
| x_ | State vector estimate. Will be destroyed. | |
| P_ | Error covariance matrix estimate. Will be destroyed. |
setDim(), setSizeX() or setSizeW() is called, then init() must be called again before any other non-dimensioning function. Definition at line 191 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeA | ( | ) | [inline, protected, virtual] |
Virtual creator of A.
Reimplemented in cPlaneEKF, and cPlaneEKF_sp.
Definition at line 503 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeAImpl | ( | ) | [inline, private] |
makeA() template method.
Definition at line 838 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseA | ( | ) | [inline, protected, virtual] |
Virtual pre-creator of A.
Reimplemented in cPlaneEKF.
Definition at line 467 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseAImpl | ( | ) | [inline, private] |
makeBaseA() template method.
Definition at line 790 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseH | ( | ) | [inline, protected, virtual] |
Virtual pre-creator of H.
Reimplemented in cPlaneEKF.
Definition at line 482 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseHImpl | ( | ) | [inline, private] |
makeBaseH() template method.
Definition at line 814 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseQ | ( | ) | [inline, protected, virtual] |
Virtual pre-creator of Q.
OQ is true, that is, if Q is always diagonal, then it is not necessary to initialize non-diagonal elements with anything meaningful. Reimplemented in cPlaneEKF.
Definition at line 477 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseQImpl | ( | ) | [inline, private] |
makeBaseQ() template method.
Definition at line 806 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseR | ( | ) | [inline, protected, virtual] |
Virtual pre-creator of R.
OVR is true, that is, if both V and R are always diagonal, then it is not necessary to initialize non-diagonal elements with anything meaningful. Reimplemented in cPlaneEKF.
Definition at line 492 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseRImpl | ( | ) | [inline, private] |
makeBaseR() template method.
Definition at line 830 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseV | ( | ) | [inline, protected, virtual] |
Virtual pre-creator of V.
OVR is true, that is, if both V and R are always diagonal, then it is not necessary to initialize non-diagonal elements with anything meaningful. Reimplemented in cPlaneEKF.
Definition at line 487 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseVImpl | ( | ) | [inline, private] |
makeBaseV() template method.
Definition at line 822 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseW | ( | ) | [inline, protected, virtual] |
Virtual pre-creator of W.
Reimplemented in cPlaneEKF.
Definition at line 472 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeBaseWImpl | ( | ) | [inline, private] |
makeBaseW() template method.
Definition at line 798 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeCommonMeasure | ( | ) | [inline, protected, virtual] |
Optional function used to precalculate common values for measurement.
If complex calculations are needed for more than one of makeH(), makeV(), makeR(), makeMeasure() and makeDZ() functions, then this function can be used to store the results in temporary variables of the derived class.
simulate() function will call this function but has no knowledge of how to undo it. Definition at line 500 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeCommonProcess | ( | ) | [inline, protected, virtual] |
Optional function used to precalculate common values for process.
If complex calculations are needed for more than one of makeA(), makeW(), makeQ() and makeProcess() functions, then this function can be used to store the results in temporary variables of the derived class.
predict() function will call this function but has no knowledge of how to undo it. Definition at line 497 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeDZ | ( | ) | [inline, protected, virtual] |
Hook-up function to modify innovation vector.
This function should rarely be overridden ; this is more of a hack than anything else. In fact, this is used to perform adjustements on the result of substracting the predicted measurement vector to the real measurement vector. This is needed, for example, when measures include angles. It may be mandatory that the difference of the two angles be in a certain range, like ![$ [-\pi, \pi] $](form_53.png) .
.
Definition at line 533 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeH | ( | ) | [inline, protected, virtual] |
Virtual creator of H.
Reimplemented in cPlaneEKF, and cPlaneEKF_sp.
Definition at line 518 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeHImpl | ( | ) | [inline, private] |
makeH() template method.
Definition at line 862 of file ekfilter_impl.hpp.
| virtual void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeMeasure | ( | ) | [protected, pure virtual] |
Actual measurement function 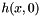 . Fills in z.
. Fills in z.
This function must be overridden, since it is the core of the measurement system. At the time this will be called, x contains the predicted state (a priori state estimate), which is the one that must be used with the measurement function.
simulate(), which does a calculation and then undoes it before returning the result. Implemented in Kalman::KFilter< T, BEG, OQ, OVR, DBG >, sample_A, cPlaneEKF, and cPlaneEKF_sp.
| virtual void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeProcess | ( | ) | [protected, pure virtual] |
Actual process 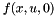 . Fills in new x by using old x.
. Fills in new x by using old x.
This function must be overridden, since it is the core of the system process.
predict(), which does a calculation and then undoes it before returning the result. Implemented in Kalman::KFilter< T, BEG, OQ, OVR, DBG >, sample_A, cPlaneEKF, and cPlaneEKF_sp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeQ | ( | ) | [inline, protected, virtual] |
Virtual creator of Q.
OQ is true, that is, if Q is always diagonal, then it is not necessary to initialize non-diagonal elements with anything meaningful. Reimplemented in cPlaneEKF_sp.
Definition at line 513 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeQImpl | ( | ) | [inline, private] |
makeQ() template method.
Definition at line 854 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeR | ( | ) | [inline, protected, virtual] |
Virtual creator of R.
OVR is true, that is, if both V and R are always diagonal, then it is not necessary to initialize non-diagonal elements with anything meaningful. Reimplemented in cPlaneEKF_sp.
Definition at line 528 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeRImpl | ( | ) | [inline, private] |
makeR() template method.
Definition at line 878 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeV | ( | ) | [inline, protected, virtual] |
Virtual creator of V.
OVR is true, that is, if both V and R are always diagonal, then it is not necessary to initialize non-diagonal elements with anything meaningful. Reimplemented in cPlaneEKF_sp.
Definition at line 523 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeVImpl | ( | ) | [inline, private] |
makeV() template method.
Definition at line 870 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeW | ( | ) | [inline, protected, virtual] |
Virtual creator of W.
Reimplemented in cPlaneEKF_sp.
Definition at line 508 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::makeWImpl | ( | ) | [inline, private] |
makeW() template method.
Definition at line 846 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::measureUpdate | ( | T | dz, | |
| T | r | |||
| ) | [inline, private] |
U-D convariance factorization update.
This function is based on an algorithm in presented in appendix V.A in [01]. It is used to generate a corrected state prediction and to update U. It must be called once per measure, with the corresponding values of H, V and R.
| dz | New (whitened) measure difference to incorporate. | |
| r | Covariance (whitened) of the measure. |
Definition at line 744 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::measureUpdateStep | ( | const Vector & | z_ | ) | [inline] |
Makes one correction step.
First, this function resizes any matrix who needs it. If z_ is empty, that is, if there are no measures in this step, there is no correction and the function stops there. Else, the measure update phase begins. This means that the following virtual functions should be called : makeCommonMeasure(), makeHImpl(), makeVImpl(), makeRImpl(), makeMeasure() and makeDZ().After this phase, x contains the new corrected state.
| z_ | Measurement vector. Will not be destroyed. Can be empty. |
Definition at line 267 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::NoModification | ( | ) | [inline, protected] |
Allows optimizations on some calculations.
By default, the EKFilter template class suppose that matrix pre-creators and creators modify all matrices. However, if it could suppose that some of these functions do not modify anything, some calculations could be optimized away. The NoModification() function says that the function in which it has been called has not modified any matrix. For optimization purposes, this means that this function should be called in every non-mutating execution branch of all make*() and makeBase*() functions.
Definition at line 462 of file ekfilter_impl.hpp.
| const KTYPENAME EKFilter< T, BEG, OQ, OVR, DBG >::Vector & Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::predict | ( | Vector & | u_ | ) | [inline] |
Returns the predicted state vector (a priori state estimate).
This function is used to predict a future state. First, it resizes any matrix who needs it. Then, it does a partial time update, in the sense that only x is updated, not P. This also means that only the following virtual functions should be called : makeCommonProcess() and makeProcess().
| u_ | Input vector. Will not be destroyed. Can be empty. |
const function). Only a copy of x is returned. Definition at line 396 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::setDim | ( | K_UINT_32 | n_, | |
| K_UINT_32 | nu_, | |||
| K_UINT_32 | nw_, | |||
| K_UINT_32 | m_, | |||
| K_UINT_32 | nv_ | |||
| ) | [inline] |
Sets all dimensions at once.
This function simply calls the setSize*() functions for x, u, w, z, v with the corresponding arguments.
setSize*() functions) must be called before any other functions. init() must always be called after this function and before any other non-dimensioning function. Definition at line 113 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::setSizeU | ( | K_UINT_32 | nu_ | ) | [inline] |
Sets the size of the input vector.
Definition at line 159 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::setSizeV | ( | K_UINT_32 | nv_ | ) | [inline] |
Sets the size of the measurement noise vector.
Definition at line 183 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::setSizeW | ( | K_UINT_32 | nw_ | ) | [inline] |
Sets the size of the process noise vector.
| nw_ | New process noise vector size. |
init() must always be called after this function and before any other non-dimensioning function. Definition at line 167 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::setSizeX | ( | K_UINT_32 | n_ | ) | [inline] |
Sets the size of the state vector.
| n_ | New state vector size. Must not be 0. |
init() must always be called after this function and before any other non-dimensioning function. Definition at line 149 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::setSizeZ | ( | K_UINT_32 | m_ | ) | [inline] |
Sets the size of the measurement vector.
Definition at line 175 of file ekfilter_impl.hpp.
| const KTYPENAME EKFilter< T, BEG, OQ, OVR, DBG >::Vector & Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::simulate | ( | ) | [inline] |
Returns the predicted measurement vector.
This function is used to predict a future measurement. First, it resizes any matrix who needs it. Then, it does a partial measure update, in the sense that only z is calculated : x and P are not updated. This also means that only the following virtual functions should be called : makeCommonMeasure() and makeMeasure().
const function. It only works on copies of vectors. Definition at line 413 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::sizeUpdate | ( | ) | [inline, protected, virtual] |
Resizes all vector and matrices. Never call or overload this !
Reimplemented in Kalman::KFilter< T, BEG, OQ, OVR, DBG >.
Definition at line 536 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::step | ( | Vector & | u_, | |
| const Vector & | z_ | |||
| ) | [inline] |
Makes one prediction-correction step.
This is the main EKFilter function. First, it resizes any matrix who needs it. Then, it proceeds to the time update phase, using the input vector u_. This means that the following virtual functions should be called : makeCommonProcess(), makeA(), makeW(), makeQ() and makeProcess(). At this stage, x contains a current predicted state instead of an old corrected state. If z_ is empty, that is, if there are no measures in this step, there is no correction and the function stops there. Else, the measure update phase begins. This means that the following virtual functions should be called : makeCommonMeasure(), makeHImpl(), makeVImpl(), makeRImpl(), makeMeasure() and makeDZ().After this phase, x contains the new corrected state.
| u_ | Input vector. Will not be destroyed. Can be empty. | |
| z_ | Measurement vector. Will not be destroyed. Can be empty. |
Definition at line 201 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::timeUpdate | ( | ) | [inline, private] |
MWG-S orthogonalization algorithm for U-D time update.
This function is based on an algorithm in presented in appendix VI.A in [01]. It is used to generate a state prediction and to update U.
Definition at line 672 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::timeUpdateStep | ( | Vector & | u_ | ) | [inline] |
Makes one prediction step.
This function first resizes any matrix who needs it. Then, it proceeds to the time update phase, using the input vector u_. This means that the following virtual functions should be called : makeCommonProcess(), makeA(), makeW(), makeQ() and makeProcess(). At this stage, x contains a current predicted state instead of an old corrected state.
| u_ | Input vector. Will not be destroyed. Can be empty. |
Definition at line 207 of file ekfilter_impl.hpp.
| void Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::upperInvert | ( | Matrix & | P_ | ) | [inline, static, private] |
Inplace upper triangular matrix inversion.
This function calculates the inverse of P_ with an efficient algorithm, based on the fact that P_ is triangular. The result of the inversion is stored in a transposed form in the lower part of P_.
| P_ | Upper triangular matrix with unit diagonal. |
Definition at line 648 of file ekfilter_impl.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::_P [mutable, private] |
Temporary matrix.
Definition at line 689 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::_x [mutable, private] |
Definition at line 690 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::a [private] |
Temporary vector.
Definition at line 681 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::A [protected] |
A jacobian matrix.
This is an n by n jacobian matrix of partial derivatives, defined as follow :
![\[ A_{[i,j]} = \frac{\partial f_{[i]}}{\partial x_{[j]}} \]](form_21.png)
Derived classes should modify it only through makeBaseA() for the constant part and makeA() for the variable part.
Definition at line 490 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::d [private] |
Temporary vector.
Definition at line 682 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::dz [protected] |
Innovation vector.
This is an m-sized vector. Derived classes should modify it only through makeDZ(). The innovation vector is the difference between the real measurement vector and the predicted one.
Definition at line 483 of file ekfilter.hpp.
K_UINT_16 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::flags [private] |
Temporary vector.
Bitfield keeping track of modified matrices.
Definition at line 692 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::H [protected] |
A jacobian matrix.
This is an m by n jacobian matrix of partial derivatives, defined as follow :
![\[ H_{[i,j]} = \frac{\partial h_{[i]}}{\partial x_{[j]}} \]](form_23.png)
Derived classes should modify it only through makeBaseH() for the constant part and makeH() for the variable part.
Definition at line 513 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::H_ [private] |
Modified version of H to whiten measure noise.
If V and R are not both diagonal, then 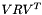 if not diagonal : measurement noise is not normalized, and must be modified for the algorithms to work. To achieve this result, we factorize it like this :
if not diagonal : measurement noise is not normalized, and must be modified for the algorithms to work. To achieve this result, we factorize it like this : 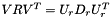 . We then replace
. We then replace 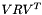 by R_
by R_ 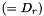 , H by H_ (
, H by H_ ( 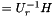 ) and dz by _x (
) and dz by _x ( 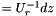 ).
).
Definition at line 665 of file ekfilter.hpp.
K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::m [protected] |
Size of the measurement vector.
Definition at line 544 of file ekfilter.hpp.
bool Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::modified_ [private] |
Boolean flag used by NoModification().
Definition at line 693 of file ekfilter.hpp.
K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::n [protected] |
Size of the state vector.
Definition at line 541 of file ekfilter.hpp.
K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::nn [private] |
Number of columns of U.
In fact, 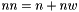 , so that U can contain W is its right part.
, so that U can contain W is its right part.
Definition at line 687 of file ekfilter.hpp.
K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::nu [protected] |
Size of the input vector.
Definition at line 542 of file ekfilter.hpp.
K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::nv [protected] |
Size of the measurement noise vector.
Definition at line 545 of file ekfilter.hpp.
K_UINT_32 Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::nw [protected] |
Size of the process noise vector.
Definition at line 543 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::Q [protected] |
Process noise covariance matrix.
This is the nw by nw covariance matrix of w, that is :
![\[ Q = E\left( w w^T \right) \]](form_54.png)
Derived classes should modify it only through makeBaseQ() for the constant part and makeQ() for the variable part. If Q is always diagonal, then you should turn on the OQ optimization.
Definition at line 506 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::Q_ [private] |
Modified version of Q to whiten process noise.
If Q is not diagonal, then process noise is correlated, and must be whitened for the algorithms to work. To achieve this result, we factorize Q like this : 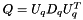 . We then replace W by W_ (
. We then replace W by W_ ( 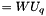 ) and Q by Q_ (
) and Q by Q_ ( 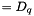 ).
).
Definition at line 655 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::R [protected] |
Measurement noise covariance matrix.
This is the nv by nv covariance matrix of v, that is :
![\[ R = E\left( v v^T \right) \]](form_55.png)
Derived classes should modify it only through makeBaseR() for the constant part and makeR() for the variable part. If both V and R are always diagonal, then you should turn on the OVR optimization.
Definition at line 531 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::R_ [private] |
Modified version of R to whiten measure noise.
If V and R are not both diagonal, then 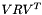 if not diagonal : measurement noise is not normalized, and must be modified for the algorithms to work. To achieve this result, we factorize it like this :
if not diagonal : measurement noise is not normalized, and must be modified for the algorithms to work. To achieve this result, we factorize it like this : 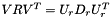 . This matrix contains the result of this factorization : the diagonal of R_ is
. This matrix contains the result of this factorization : the diagonal of R_ is 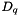 , the upper part is
, the upper part is 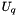 (the unit diagonal is implied) and the lower part is
(the unit diagonal is implied) and the lower part is 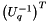 (the unit diagonal is again implied).
(the unit diagonal is again implied).
If both V and R are diagonal, then 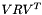 is diagonal. In that case, R_ is in fact
is diagonal. In that case, R_ is in fact 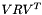 .
.
Definition at line 679 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::U [private] |
Cholesky factorization of P.
This matrix is the upper triangular Cholesky factorization of P. So, it should be a n by n matrix, but because of algorithmic issues, it is in fact a n by nn matrix. Usually, the factorization would yield two matrices, U and D ( 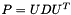 ), where U is an upper triangular matrix with unit diagonal, and D is a diagonal matrix. Since the unit diagonal is implicit in our representation, this matrix contains D on its diagonal, U in its upper part and junk in its lower part. This is for the left n by n part of the matrix. For the right n by nw part, it is mainly junk, but it is used temporarily to hold a copy of W.
), where U is an upper triangular matrix with unit diagonal, and D is a diagonal matrix. Since the unit diagonal is implicit in our representation, this matrix contains D on its diagonal, U in its upper part and junk in its lower part. This is for the left n by n part of the matrix. For the right n by nw part, it is mainly junk, but it is used temporarily to hold a copy of W.
Definition at line 643 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::u [protected] |
Input vector.
This is an nu-sized vector. Derived classes should never modify it.
Definition at line 474 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::v [private] |
Temporary vector.
Definition at line 683 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::V [protected] |
A jacobian matrix.
This is an m by nv jacobian matrix of partial derivatives, defined as follow :
![\[ V_{[i,j]} = \frac{\partial h_{[i]}}{\partial v_{[j]}} \]](form_24.png)
Derived classes should modify it only through makeBaseV() for the constant part and makeV() for the variable part. If both V and R are always diagonal, then you should turn on the OVR optimization.
Definition at line 522 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::W [protected] |
A jacobian matrix.
This is an n by nw jacobian matrix of partial derivatives, defined as follow :
![\[ W_{[i,j]} = \frac{\partial f_{[i]}}{\partial w_{[j]}} \]](form_22.png)
Derived classes should modify it only through makeBaseW() for the constant part and makeW() for the variable part.
Definition at line 497 of file ekfilter.hpp.
Matrix Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::W_ [private] |
Modified version of W to whiten process noise.
If Q is not diagonal, then process noise is correlated, and must be whitened for the algorithms to work. To achieve this result, we factorize Q like this : 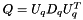 . We then replace W by W_ (
. We then replace W by W_ ( 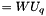 ) and Q by Q_ (
) and Q by Q_ ( 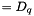 ).
).
Definition at line 649 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::x [protected] |
Corrected state vector.
This is an n-sized vector. Derived classes should modify it only through makeProcess().
Definition at line 470 of file ekfilter.hpp.
Vector Kalman::EKFilter< T, BEG, OQ, OVR, DBG >::z [protected] |
Predicted measurement vector.
This is an m-sized vector. Derived classes should modify it only through makeMeasure().
Definition at line 478 of file ekfilter.hpp.