Generic Linear Kalman Filter template base class. More...
#include <kfilter.hpp>

Public Member Functions | |
| virtual | ~KFilter ()=0 |
| Virtual destructor. | |
Protected Member Functions | |
| virtual void | makeB () |
| Virtual creator of B. | |
| virtual void | makeBaseB () |
| Virtual pre-creator of B. | |
Protected Attributes | |
| Matrix | B |
| Input matrix. | |
Private Member Functions | |
| virtual void | makeMeasure () |
| Measurement function overridden to be linear. | |
| virtual void | makeProcess () |
| Process function overridden to be linear. | |
| virtual void | sizeUpdate () |
| Matrix and vector resizing function, overridden to take B into account. | |
Private Attributes | |
| Vector | x__ |
| Temporary vector. | |
Generic Linear Kalman Filter template base class.
EKFilter. You should really read all the documentation of EKFilter before reading this. EKFilter template class.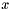 (to estimate) and a linear process function
(to estimate) and a linear process function 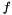 (to model) that describes the evolution of this state through time, that is :
(to model) that describes the evolution of this state through time, that is :
![\[ x_k = f \left( x_{k-1}, u_{k-1}, w_{k-1} \right) = //! A x_{k-1} + B u_{k-1} + W w_{k-1} \]](form_70.png)
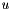 is the (known) input vector fed to the process and
is the (known) input vector fed to the process and 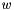 is the (unknown) process noise vector due to uncertainty and process modeling errors. Further suppose that the (known) process noise covariance matrix is :
is the (unknown) process noise vector due to uncertainty and process modeling errors. Further suppose that the (known) process noise covariance matrix is :
![\[ Q = E \left( w w^T \right) \]](form_39.png)
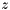 , which depends on the current state
, which depends on the current state 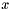 in the form of a linear function
in the form of a linear function 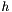 (to model) :
(to model) :
![\[ z_k = h \left( x_k, v_k \right) = //! H x_k + V v_k \]](form_71.png)
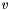 is the (unknown) measurement noise vector with a (known) covariance matrix :
is the (unknown) measurement noise vector with a (known) covariance matrix :
![\[ R = E \left( v v^T \right) \]](form_42.png)
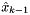 , called a corrected state or an a posteriori state estimate. We can build a predicted state (also called an a priori state estimate) by using
, called a corrected state or an a posteriori state estimate. We can build a predicted state (also called an a priori state estimate) by using 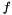 :
:
![\[ \tilde{x}_k = f \left( \hat{x}_{k-1}, u_{k-1}, 0 \right) = //! A \hat{x}_{k-1} + B u_{k-1} \]](form_72.png)
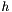 :
:
![\[ \tilde{z}_k = h \left( \tilde{x}_k, 0 \right) = //! H \tilde{x}_k \]](form_73.png)
makeProcess() and makeMeasure() have already been overridden, and cannot be ovverridden again. However, there is a new matrix to create : B. This means there are two new virtual functions that can be overridden : makeBaseB() and makeB(). EKFilter Definition at line 82 of file kfilter.hpp.
| Kalman::KFilter< T, BEG, OQ, OVR, DBG >::~KFilter | ( | ) | [inline, pure virtual] |
Virtual destructor.
Definition at line 36 of file kfilter_impl.hpp.
| void Kalman::KFilter< T, BEG, OQ, OVR, DBG >::makeB | ( | ) | [inline, protected, virtual] |
Virtual creator of B.
Definition at line 42 of file kfilter_impl.hpp.
| void Kalman::KFilter< T, BEG, OQ, OVR, DBG >::makeBaseB | ( | ) | [inline, protected, virtual] |
Virtual pre-creator of B.
Definition at line 39 of file kfilter_impl.hpp.
| void Kalman::KFilter< T, BEG, OQ, OVR, DBG >::makeMeasure | ( | ) | [inline, private, virtual] |
Measurement function overridden to be linear.
Implements Kalman::EKFilter< T, BEG, OQ, OVR, DBG >.
Definition at line 70 of file kfilter_impl.hpp.
| void Kalman::KFilter< T, BEG, OQ, OVR, DBG >::makeProcess | ( | ) | [inline, private, virtual] |
Process function overridden to be linear.
Implements Kalman::EKFilter< T, BEG, OQ, OVR, DBG >.
Definition at line 45 of file kfilter_impl.hpp.
| void Kalman::KFilter< T, BEG, OQ, OVR, DBG >::sizeUpdate | ( | ) | [inline, private, virtual] |
Matrix and vector resizing function, overridden to take B into account.
Reimplemented from Kalman::EKFilter< T, BEG, OQ, OVR, DBG >.
Definition at line 88 of file kfilter_impl.hpp.
Matrix Kalman::KFilter< T, BEG, OQ, OVR, DBG >::B [protected] |
Input matrix.
Definition at line 49 of file kfilter.hpp.
Vector Kalman::KFilter< T, BEG, OQ, OVR, DBG >::x__ [private] |
Temporary vector.
Definition at line 63 of file kfilter.hpp.